Introduction
In this article we will investigate the consideration of Cabinet Stiffness as a possibility to justify the reduction of the pressure sustained by an enclosed Cabinet in case of decompression.
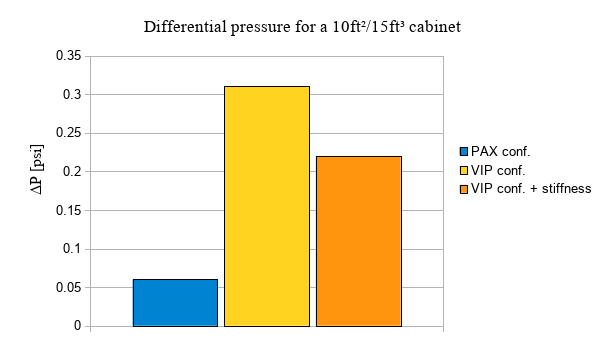
We will then consider a dummy Cabinet (Vol#02) with Volume of 15ft³ and Vent Area of 10in² installed in same room (Bedroom - Vol#01) of the VIP Configuration of our numeric Corporate Jet. As shown in the results table of Article #4, the pressure sustained by this cabinet is 0.31psi.
Cabinet FE Model
In order to quickly evaluate a possible evolution of the cabinet venting area with the applied differential pressure a Finite Element model of a simple cabinet was built. The cabinet material considered was a standard 1/2 inch honeycomb panel (doors included). The cabinet size was defined to get an equivalent total volume is 15ft³ (36inx48inx15in). The gap around the doors was adjusted to get a total Vent Area close to 10in² (see door gap area highlighted in the figure below).
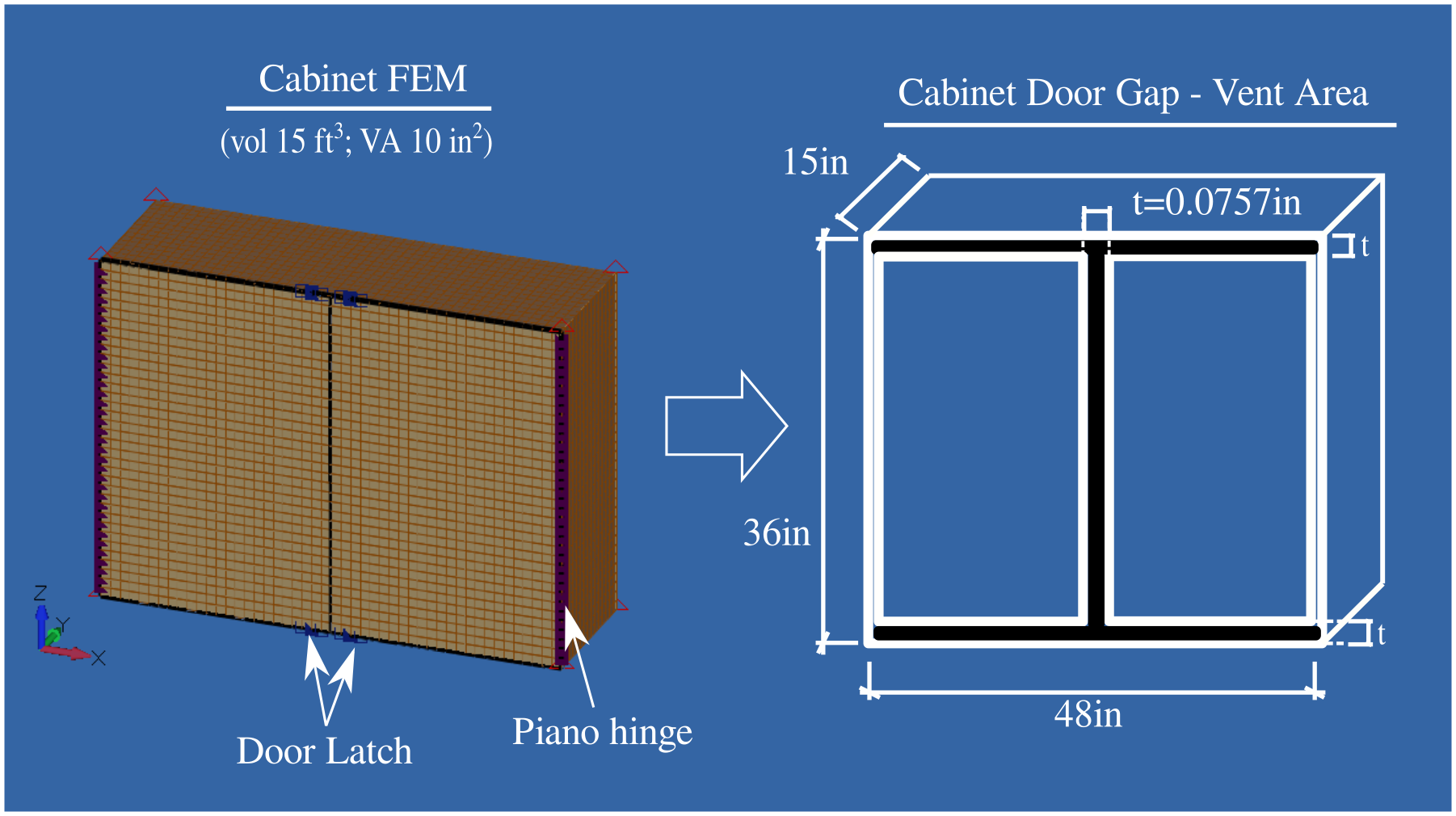
The doors are mounted to the cabinet with piano hinges (Rz rotation is possible) and are locked with latches (fixed in Tx, Ty). The cabinet is fixed at its eight corners (nodes fixed constraints). The differential pressure sustained by the Cabinet (\(\Delta_P\)) is applied as element pressure.
As a first approach a linear analysis is performed to get the evolution of Vent Area due to the doors and cabinet body deformation under applied pressure.
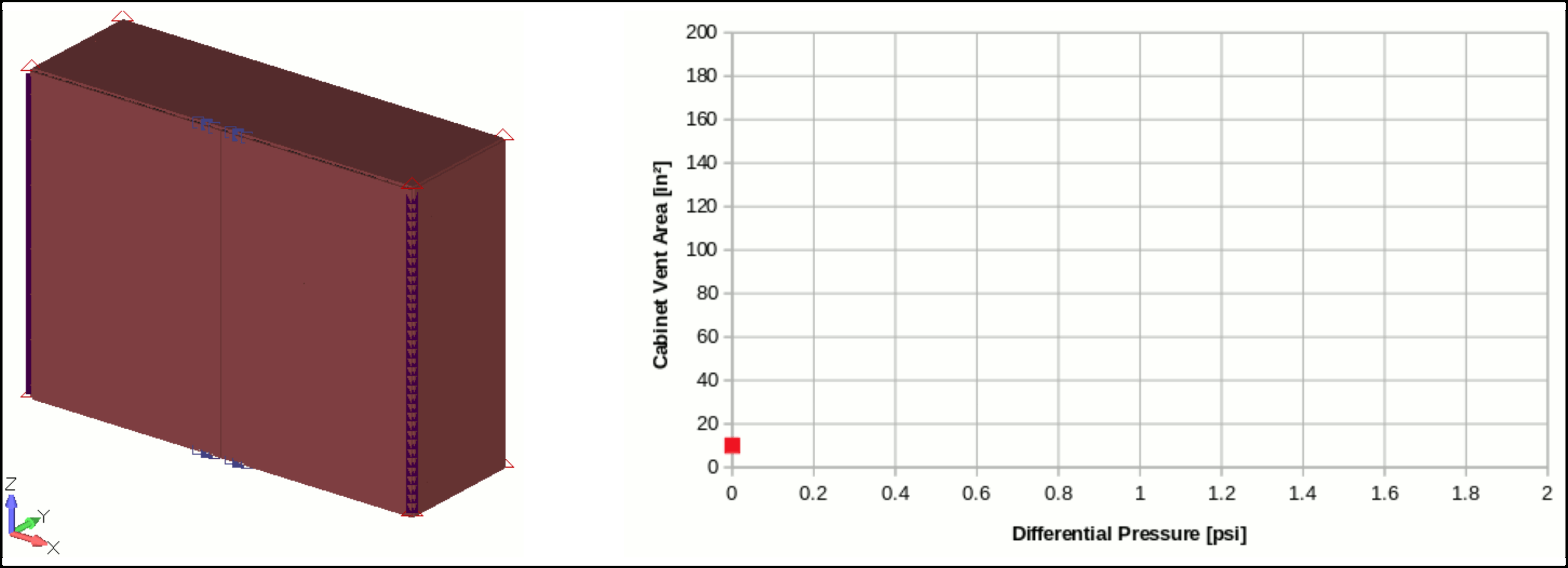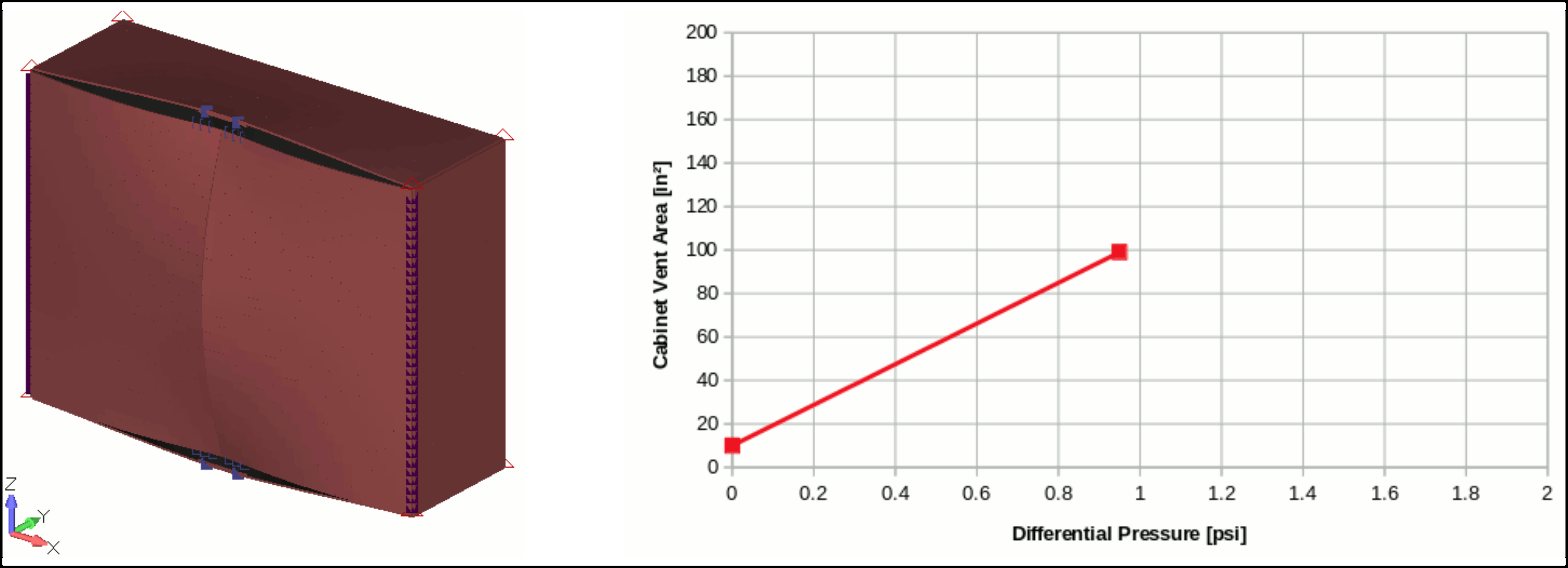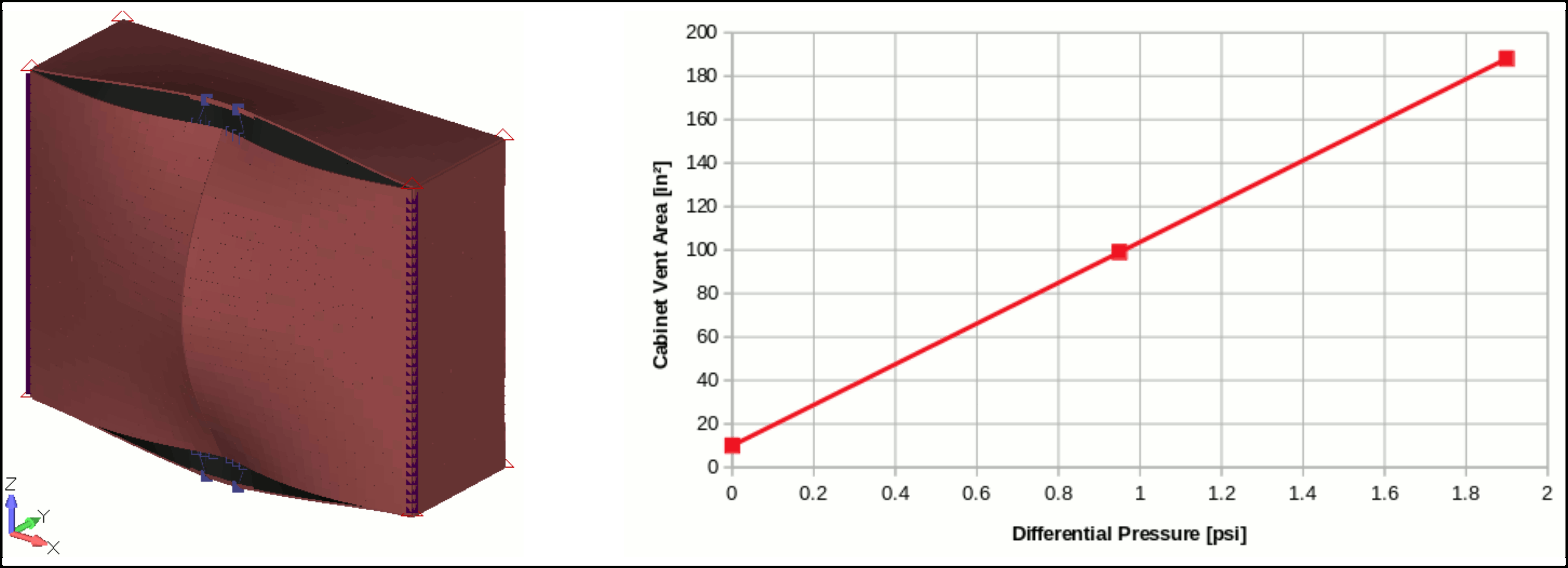
The evolution of the cabinet Vent Area can be easily related to the applied pressure with the following equation:
Equation 1:
Where:
- Total Vent: V [in²] depending on applied differential pressure \(\Delta_P\)
- Passive Vent: \(V_{0}=10in²\) (initial Cabinet Vent Area, Gap around doors)
- Active Vent: \(V_{a}=K_{n}\cdot \Delta_P\) with \(K_{n}=93.6in⁴/lbf\) (Slope of the curve Vent Area Vs \(\Delta_P\)).
In our example:
\(V = 10 + 93.6 \cdot \Delta_P\)
NOTE: With an applied differential pressure of \(\Delta_P=0.11psi\) the cabinet Vent Area is already doubled compared to its initial value of 10in².
Esonix Stiffness
In order to implement the evolution of the Cabinet Vent Area with the applied differential pressure during the course of the decompression analysis, ESonix Dynamical Attributes will be used. In ESonix, decompression features like flaps, panels and doors can dynamically open during decompression run time integrating parameters like their inertia, spring stiffness, air drag, etc…
NOTE: Those Dynamical attributes are accessible through “tab Dyn_Attibutes” on the Esonix Advanced Template. Additional information are available on User Manual (see Manuals) and Advanced Manual.
In our example, the dynamical increase of the cabinet Vent Area will be simulated with an equivalent translational panel held by a spring of stiffness Ke. This spring stiffness Ke needs to be adjusted such as the opening of this panel matches the active vent curve derived from the FE analysis. Therefore a stiffness equivalence between Kn (Cabinet Vent Area from FEA, see equation 1 above) and Ke (Esonix stiffness of translating panel) needs to be established.
The figure below shows a hypothetical panel (representing our Cabinet Active Vent Area) with main dimensions a and b and sustaining a pressure \(\Delta_P\). The Esonix spring stiffness (Ke) is also shown in the same figure.
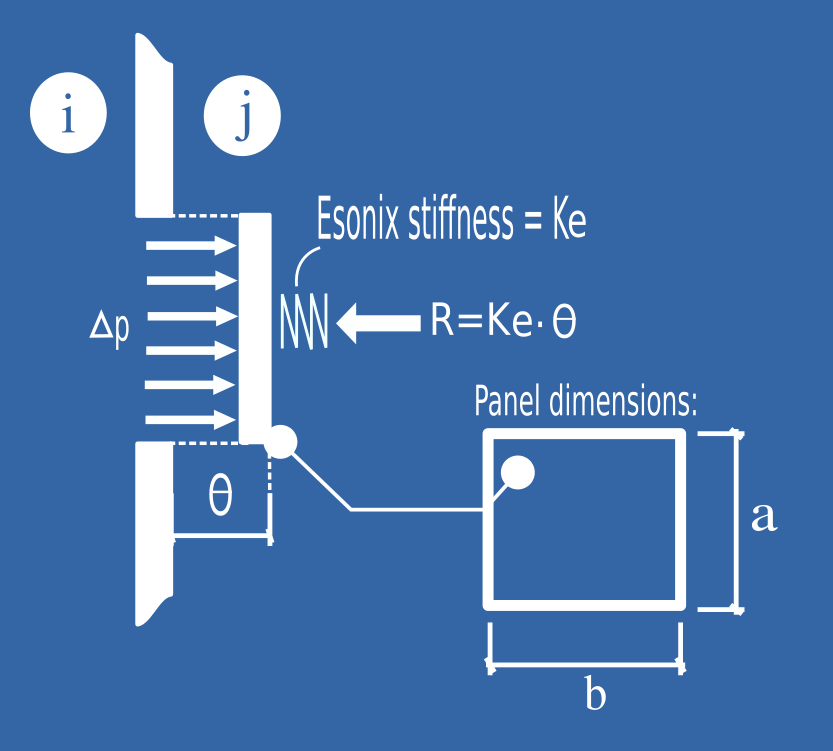
Through the figure above, the Active Vent Area (Va) can be written in function of the Displacement (\(\theta\)), as per equations 2 and 3 below. The Forces Balance leads us to the equation 4 also shown below.
Vent Area (V) function of Displacement θ
Equation 2 (Active Vent Area proportional to the panel peripheral opening area):
Equation 3:
Forces Balance assuming negligible mass
Equation 4:
Finally the equations 3 and 4 can be combined in 5 which leads us to an equation where the Vent Area (V) is written in function of \(\Delta_P\).
Equation 5:
Stiffness Equivalence
At this point we have equations 1 and 5 where Active Vent Area (Va) is written in function of \(\Delta_P\). Through those equations, the stiffness equivalence between Ke (Esonix stiffness) and Kn (stiffness from Cabinet FEM) can be defined as:
Equation 6:
Based on the equation above, we can now define the Esonix Stiffness (Ke) to be considered in our Esonix Decompression Model.
As a=10in², b=10in² and Kn=93.6in⁴/lbf:
Results and Conclusion
Considering the connections and Dyn_Attibutes modifications proposed above, after a run with Esonix software, the pressure sustained by the cabinet, when its stiffness is considered is down to 0.22psi.
As shown in the Article #4, the pressure sustained by the same cabinet (Vol = 15ft³ and VA =10in²) in the same aircraft VIP configuration and not considering the cabinet stiffness, is 0.31psi.
From results tables in Article #3 , the pressure sustained by the same cabinet (vol=15ft³ and VA=10in²) in a PAX configuration (therefore installed in a wider room) is 0.06psi.
As conclusion, we can highlight that considering the Cabinet stiffness can be an effective approach to decrease the pressure sustained by a Cabinet in refurbishment projects.
As demonstrated in this Article, through the Dynamical Attributes offered by Esonix, the cabinet stiffness can be easily considered in the decompression analysis.
Decompression Model considering the Cabinet Stiffness
Download the ESonix numeric Corporate Jet in its vip configuration - Cabinet with stiffness.
Our VIP configuration model considers a dummy Cabinet (Vol#02) with Volume of 15ft³ and Vent Area of 10in² installed in same room (Bedroom - Vol#01), see Article #4 for more details.
As previously explained, the Vent Area (connections) between the Cabinet (Vol#02) and the Bedroom (Vol#01) is splitted in two parts: Passive Vent and Active Vent, as shown below.
id vol_i vol_j comments vent_area open.pressure cp
j_to_i j_to_i j_to_i
[in²] [psi] [-]
100 1 2 Cabinet to Bedroom - passive 10 0 0.60
101 1 2 Cabinet to Bedroom - active 1 0.001 0.60
The Active Vent considers a small value for the Opening Pressure which means that this vent will be activated since the beginning. Its Vent Area value of 1 in2 will vary according to the stiffness settled on “Dyn_Attributes” sheet and to \(\Delta_P\).
By the Esonix sheet “Dyn_Attributes”, the Cabinet stiffness can then be considered as shown:
id axis a b mass stiffness
[in] [in] [lbs] [lbf/in]
101 2 10 10 0 42.7
where:
- id #101 refers to connection #101 - active Vent Area between the Cabinet and Bedroom
- axis = 2 is corresponding to translational panel
- a = b = 10in are dummy dimensions of the panel. It can assume any value since they are also considered in the calculation of Ke
- mass = 0 mass is not a relevant parameter in this analysis
- stiffness = 42.7 (lbf/in) is the equivalent spring stiffness calculated previously.
See here the list of Articles referring to the study of Small Volume Decompression:
-
Article #1: Small Volumes Decompression #1 - Understanding the Problem
-
Article #2: Small Volumes Decompression #2 - Airline/Pax, VIP configurations and Aircraft Parameters
-
Article #3: Small Volumes Decompression #3 - Analysis of closed compartment in the Cabin Airline/PAX Configuration
-
Article #4: Small Volumes Decompression #4 - Analysis of closed compartment in the Cabin VIP Configuration
-
Article #5: Small Volumes Decompression #5 - Airline X VIP Results Comparison
-
Article #6: Small Volumes Decompression #6 - Airline X VIP Results Comparison (Further Step)
-
Article #7: Small Volumes Decompression #7 - Decompression Analysis considering the Cabinet Stiffness
-
Article #8: Small Volumes Decompression #8 - Study summary and conclusions